--- title: Regression Analysis | Examples of Regression Models | Statgraphics description: Regression analysis is used to model the relationship between a response variable and one or more predictor variables. Learn ways of fitting models here! --- [![Statgraphics 19 logo](https://www.statgraphics.com/hs-fs/hubfs/stat19plain-01-1.png?width=2272&height=484&name=stat19plain-01-1.png "Statgraphics 19 logo")](https://www.statgraphics.com) - [Products](https://www.statgraphics.com/product) - [Learn](https://www.statgraphics.com/statistics-library) - [Training](https://www.statgraphics.com/training-and-consulting) - [Product](https://www.statgraphics.com/product) - [Centurion XVIII](https://www.statgraphics.com/centurion-xvii) - [Sigma Express](https://www.statgraphics.com/statgraphics-sigma-express) - [Online](https://www.statgraphics.com/statgraphics-stratus) - [Web Services](https://www.statgraphics.com/statgraphics-web-services) - [Learn](https://www.statgraphics.com/statistics-library) - [Statistics Library](https://www.statgraphics.com/statistics-library) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Instructional Videos](https://www.statgraphics.com/instructional-videos) - [Applications/ Case Studies](https://www.statgraphics.com/application) - [Training & Consulting](https://www.statgraphics.com/training-and-consulting) - [Statpoint Seminars](https://www.statgraphics.com/statpoint-seminar) - [Statpoint Instructors](https://www.statgraphics.com/statpoint-instructor) - [Training Partners](https://www.statgraphics.com/training-partners) - [Webinars](https://www.statgraphics.com/webinars) - [Support](https://www.statgraphics.com/customer-support-overview) - [Blog](https://www.statgraphics.com/blog) - [Store](http://store.statgraphics.com) ### Statgraphics ## [Centurion](https://www.statgraphics.com/centurion-overview) #### [LEARN MORE](https://www.statgraphics.com/centurion-overview) ### Statgraphics ## [Sigma *express*](https://www.statgraphics.com/statgraphics-sigma-express) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-sigma-express) ### Statgraphics ## [*Stratus*](https://www.statgraphics.com/statgraphics-stratus) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-stratus) ### Statgraphics ## [Web Services](https://www.statgraphics.com/statgraphics-web-services) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-web-services) ## [Statistics Library](https://www.statgraphics.com/statistics-library) #### [LEARN MORE](https://www.statgraphics.com/statistics-library) ## [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) #### [LEARN MORE](https://www.statgraphics.com/six-sigma-lean) ## [Instructional Videos](https://www.statgraphics.com/instructional-videos) #### [LEARN MORE](https://www.statgraphics.com/instructional-videos) ## [Applications/ Case Studies](https://www.statgraphics.com/statistical-applications) #### [LEARN MORE](https://www.statgraphics.com/statistical-applications) ## [Statgraphics Seminars](https://www.statgraphics.com/statpoint-seminar) #### [LEARN MORE](https://www.statgraphics.com/statpoint-seminar) ## [Statgraphics Instructors](https://www.statgraphics.com/statpoint-instructor) #### [LEARN MORE](https://www.statgraphics.com/statpoint-instructor) ## [Training Partners](https://www.statgraphics.com/public-seminar) #### [LEARN MORE](https://www.statgraphics.com/public-seminar) ## [Webinars](https://www.statgraphics.com/webinars) #### [LEARN MORE](https://www.statgraphics.com/webinars) #### Statistical Capabilities - [Analysis of Variance](https://www.statgraphics.com/analysis-of-variance) - [Basic Statistical Methods](https://www.statgraphics.com/basic-statistical-methods) - [Categorical Data Analysis](https://www.statgraphics.com/categorical-data-analysis) - [Data Mining & Machine Learning](https://www.statgraphics.com/data-mining) - [Design of Experiments](https://www.statgraphics.com/design-of-experiments) - [Exploratory Data Analysis](https://www.statgraphics.com/exploratory-data-analysis) - [Life Data Analysis & Reliability](https://www.statgraphics.com/life-data-analysis-and-reliability) - [Measurement Systems Analysis](https://www.statgraphics.com/measurement-systems-analysis) - [Monte Carlo Simulation](https://www.statgraphics.com/monte-carlo) - [Multivariate Methods](https://www.statgraphics.com/multivariate-methods) - [Nonparametric Methods](https://www.statgraphics.com/nonparametric-methods) - [Probability Distributions](https://www.statgraphics.com/probability-distributions) - [Process Capability Analysis](https://www.statgraphics.com/process-capability-analysis) - [Regression Analysis](https://www.statgraphics.com/regression-analysis) - [Sample Size Determination](https://www.statgraphics.com/sample-size-determination) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Statistical Process Control Charts](https://www.statgraphics.com/statistical-process-control-charts) - [Time Series Analysis & Forecasting](https://www.statgraphics.com/time-series-analysis-and-forecasting) - [Visualization](https://www.statgraphics.com/visualization) # Regression Analysis Regression analysis is used to model the relationship between a response variable and one or more predictor variables. STATGRAPHICS Centurion provides a large number of procedures for fitting different types of regression models: [![Start Using Statgraphics Today!](https://no-cache.hubspot.com/cta/default/402067/interactive-175241846398.png)](https://www.statgraphics.com/hs/cta/wi/redirect?encryptedPayload=AVxigLLRHKR0d1vw1kvXz30coXe0b43N1bO07RvT53SuB8e1v2cAIKhZbsrr1lrYoJoddO5IU3%2B15Riys67rwhC%2Fevmlg4Yamp0udiiv7oNVFbq32hjX4DCCaY8%2B5ARCscBiRB310Kt0Nd5HstfkfVElu1r2QymD87E1Vs49a6KBjAjvfQ%2BHXKUXOb0NXo%2F4e1qUzHsxn%2FrXLCr7sHt1Mg%3D%3D&webInteractiveContentId=175241846398&portalId=402067) | Procedure | Statgraphics Centurion 18/19 | Statgraphics Sigma *express* | Statgraphics *stratus* | Statgraphics Web Services | StatBeans | | --- | --- | --- | --- | --- | --- | | [Simple Regression](https://www.statgraphics.com/regression-analysis#Simple%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Box-Cox Transformations](https://www.statgraphics.com/regression-analysis#Box-Cox%20Transformations) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | [Polynomial Regression](https://www.statgraphics.com/regression-analysis#Polynomial%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Calibration Models](https://www.statgraphics.com/regression-analysis#Calibration%20Models) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Multiple Regression](https://www.statgraphics.com/regression-analysis#Multiple%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Comparison of Regression Lines](https://www.statgraphics.com/regression-analysis#Comparison%20of%20Regression%20Lines) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Regression Model Selection](https://www.statgraphics.com/regression-analysis#Regression%20Model%20Selection) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Ridge Regression](https://www.statgraphics.com/regression-analysis#Ridge%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Nonlinear Regression](https://www.statgraphics.com/regression-analysis#Nonlinear%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Partial Least Squares](https://www.statgraphics.com/regression-analysis#Partial%20Least%20Squares) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [General Linear Models](https://www.statgraphics.com/regression-analysis#General%20Linear%20Models) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Life Data Regression](https://www.statgraphics.com/regression-analysis#Life%20Data%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Regression Analysis for Proportions](https://www.statgraphics.com/regression-analysis#Regression%20Analysis%20for%20Proportion) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Regression Analysis for Counts](https://www.statgraphics.com/regression-analysis#Regression%20Analysis%20for%20Counts) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Orthogonal Regression](https://www.statgraphics.com/regression-analysis#Orthogonal%20Regression) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Classification and Regression Trees](https://www.statgraphics.com/regression-analysis#Trees) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Piecewise Linear Regression](https://www.statgraphics.com/regression-analysis#piecewise)(V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Quantile Regression](https://www.statgraphics.com/regression-analysis#quantile)(V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Stability Studies](https://www.statgraphics.com/regression-analysis#stability) (V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | | | [Zero-Inflated Count Regression](https://www.statgraphics.com/regression-analysis#zip) (V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | | | |   #### Simple Regression 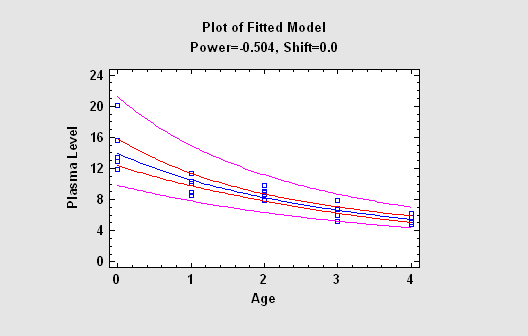The simplest regression models involve a single response variable Y and a single predictor variable X. STATGRAPHICS will fit a variety of functional forms, listing the models in decreasing order of R-squared. If outliers are suspected, resistant methods can be used to fit the models instead of least squares.  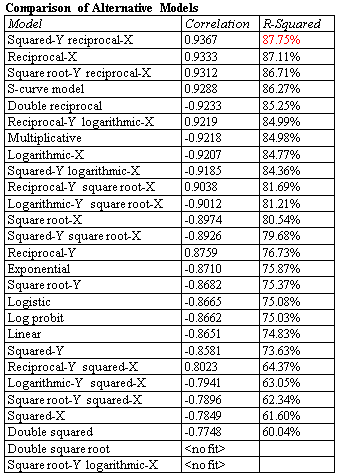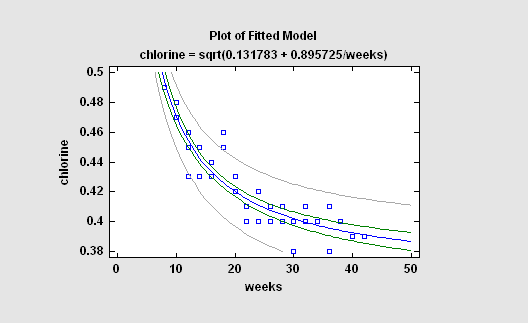![sreg2.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/sreg2.png?width=339&height=476&name=sreg2.png) ![sreg1.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/sreg1.png?width=640&name=sreg1.png "sreg1.png") More:[Simple Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Simple_Regression_1-1.pdf)   #### Box-Cox Transformations When the response variable does not follow a normal distribution, it is sometimes possible to use the methods of Box and Cox to find a transformation that improves the fit. Their transformations are based on powers of Y. STATGRAPHICS will automatically determine the optimal power and fit an appropriate model. ![boxcox.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/boxcox.png?width=640&name=boxcox.png "boxcox.png") More:[Box-Cox Transformations.pdf](https://www.statgraphics.com/hubfs/PDFs/Box-Cox_Transformations.pdf)   [![Sign Up for Special Offers](https://no-cache.hubspot.com/cta/default/402067/f26a5e52-963b-43b8-b1d8-23139cf3e7e2.png)](https://cta-redirect.hubspot.com/cta/redirect/402067/f26a5e52-963b-43b8-b1d8-23139cf3e7e2)   #### Polynomial Regression Another approach to fitting a nonlinear equation is to consider polynomial functions of X. For interpolative purposes, polynomials have the attractive property of being able to approximate many kinds of functions. 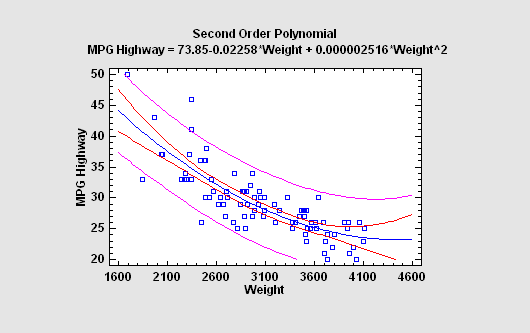![polyreg.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/polyreg.png?width=640&name=polyreg.png "polyreg.png") More:[Polynomial Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Polynomial_Regression.pdf)   #### Calibration Models In a typical calibration problem, a number of known samples are measured and an equation is fit relating the measurements to the reference values. The fitted equation is then used to predict the value of an unknown sample by generating an inverse prediction (predicting X from Y) after measuring the sample. 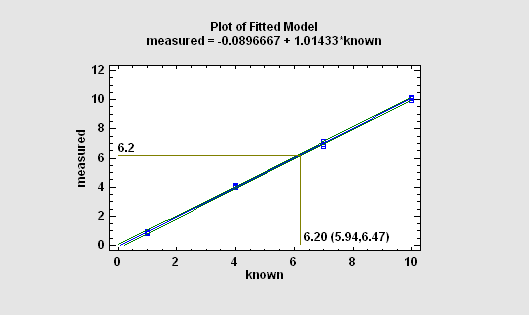![calibrate.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/calibrate.png?width=640&name=calibrate.png "calibrate.png") More:[Calibration Models.pdf](https://www.statgraphics.com/hubfs/PDFs/Calibration_Models.pdf)   #### Multiple Regression The Multiple Regression procedure fits a model relating a response variable Y to multiple predictor variables X1, X2, ... . The user may include all predictor variables in the fit or ask the program to use a stepwise regression to select a subset containing only significant predictors. At the same time, the Box-Cox method can be used to deal with non-normality and the Cochrane-Orcutt procedure to deal with autocorrelated residuals. ![mreg.png](https://www.statgraphics.com/hubfs/migrated-pages-image/mreg.png) More:[Multiple Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Multiple_Regression.pdf)   #### Comparison of Regression Lines In some situations, it is necessary to compare several regression lines. STATGRAPHICS will fit parallel or non-parallel linear regressions for each level of a "BY" variable and perform statistical tests to determine whether the intercepts and/or slopes of the lines are significantly different. 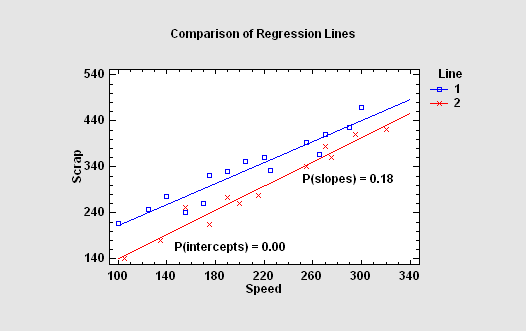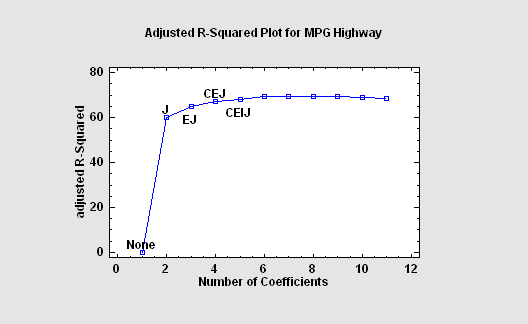![compreg.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/compreg.png?width=640&name=compreg.png "compreg.png") More:[Comparison of Regression Lines.pdf](https://www.statgraphics.com/hubfs/PDFs/Comparison_of_Regression_Lines.pdf) #### Regression Model Selection If the number of predictors is not excessive, it is possible to fit regression models involving all combinations of 1 predictor, 2 predictors, 3 predictors, etc, and sort the models according to a goodness-of fit statistic. In STATGRAPHICS, the Regression Model Selection procedure implements such a scheme, selecting the models which give the best values of the adjusted R-Squared or of Mallows' Cp statistic. ![regsel-1.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/regsel-1.png?width=640&name=regsel-1.png "regsel-1.png") More:[Regression Model Selection.pdf](https://www.statgraphics.com/hubfs/PDFs/Regression_Model_Selection.pdf)   #### Ridge Regression When the predictor variables are highly correlated amongst themselves, the coefficients of the resulting least squares fit may be very imprecise. By allowing a small amount of bias in the estimates, more reasonable coefficients may often be obtained. Ridge regression is one method to address these issues. Often, small amounts of bias lead to dramatic reductions in the variance of the estimated model coefficients. 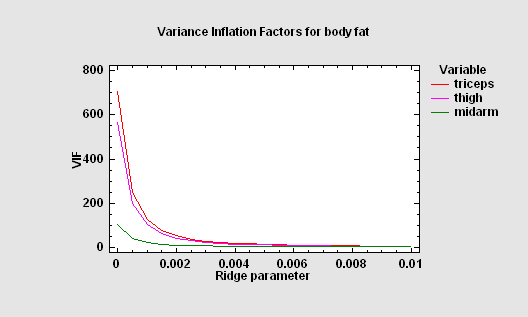![ridge.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/ridge.png?width=640&name=ridge.png "ridge.png") More:[Ridge Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Ridge_Regression.pdf)   #### Nonlinear Regression Most least squares regression programs are designed to fit models that are linear in the coefficients. When the analyst wishes to fit an intrinsically nonlinear model, a numerical procedure must be used. The STATGRAPHICS Nonlinear Least Squares procedure uses an algorithm due to Marquardt to fit any function entered by the user. ![nonlin.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/nonlin.png?width=485&height=410&name=nonlin.png) More:[Nonlinear Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Nonlinear_Regression.pdf)   #### Partial Least Squares Partial Least Squares is designed to construct a statistical model relating multiple independent variables X to multiple dependent variables Y. The procedure is most helpful when there are many predictors and the primary goal of the analysis is prediction of the response variables. Unlike other regression procedures, estimates can be derived even in the case where the number of predictor variables outnumbers the observations. PLS is widely used by chemical engineers and chemometricians for spectrometric calibration. 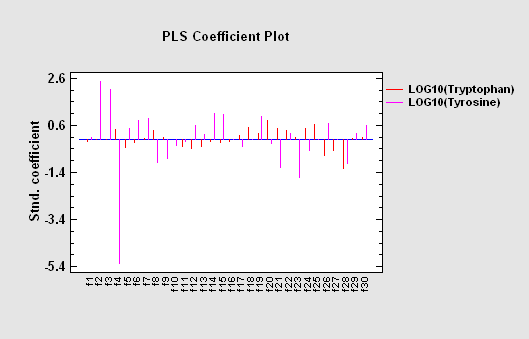![pls\_1.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/pls_1.png?width=640&name=pls_1.png "pls_1.png") More:[Partial Least Squares.pdf](https://www.statgraphics.com/hubfs/PDFs/Partial_Least_Squares_1.pdf)   #### General Linear Models The GLM procedure is useful when the predictors include both quantitative and categorical factors. When fitting a regression model, it provides the ability to create surface and contour plots easily. 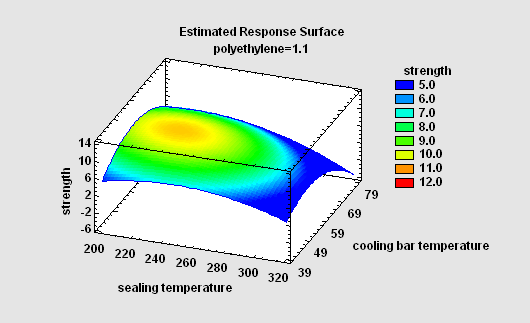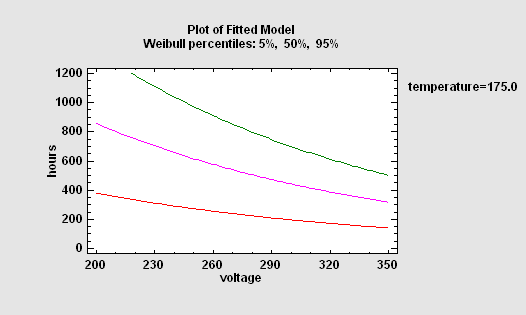![glm1.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/glm1.png?width=640&name=glm1.png "glm1.png") More:[General Linear Models.pdf](https://www.statgraphics.com/hubfs/PDFs/General_Linear_Models.pdf)   #### Life Data Regression To describe the impact of external variables on failure times, regression models may be fit. Unfortunately, standard least squares techniques do not work well for two reasons: the data are often censored, and the failure time distribution is rarely Gaussian. For this reason, STATGRAPHICS provides a special procedure that will fit life data regression models with censoring, assuming either an exponential, extreme value, logistic, loglogistic, lognormal, normal or Weibull distribution. ![lifereg.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/lifereg.png?width=640&name=lifereg.png "lifereg.png") More:[Life Data Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Life_Data_Regression_1.pdf)   #### Regression Analysis for Proportions When the response variable is a proportion or a binary value (0 or 1), standard regression techniques must be modified. STATGRAPHICS provides two important procedures for this situation: Logistic Regression and Probit Analysis. Both methods yield a prediction equation that is constrained to lie between 0 and 1. 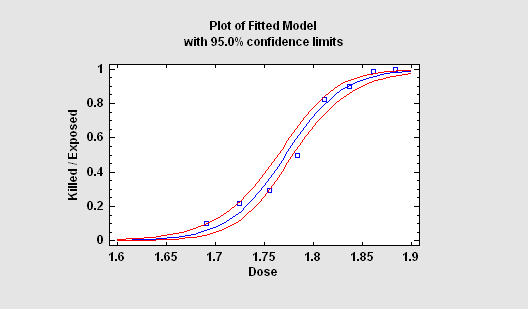![logit.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/logit.png?width=640&name=logit.png "logit.png") More:[Logistic Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Logistic_Regression.pdf),[Probit Analysis.pdf](https://www.statgraphics.com/hubfs/PDFs/Probit_Analysis.pdf)   #### Regression Analysis for Counts For response variables that are counts, STATGRAPHICS provides two procedures: a Poisson Regression and a Negative Binomial Regression. Each fits a loglinear model involving both quantitative and categorical predictors. 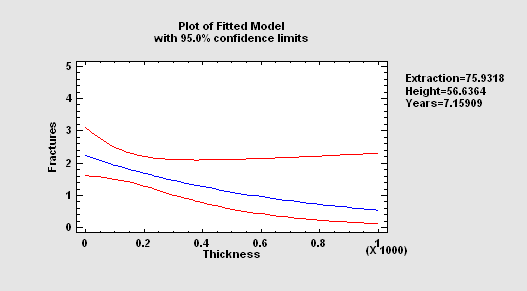![poisson.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/poisson.png?width=640&name=poisson.png "poisson.png") More:[Poisson Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Poisson_Regression.pdf),[Negative Binomial Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Negative_Binomial_Regression.pdf) **Orthogonal Regression** The Orthogonal Regression procedure is designed to construct a statistical model describing the impact of a single quantitative factor X on a dependent variable Y, when both X and Y are observed with error. Any of 27 linear and nonlinear models may be fit. 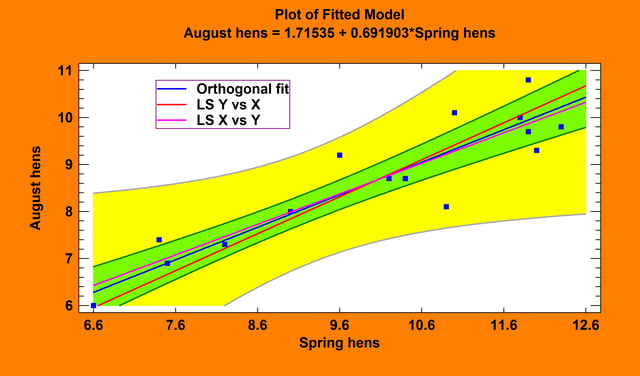![orthreg1.png](https://www.statgraphics.com/hs-fs/hubfs/orthreg1.png?width=640&name=orthreg1.png "orthreg1.png") More: [Orthogonal Regression.pdf](https://www.statgraphics.com/hubfs/PDFs/Orthogonal_Regression.pdf) or [watch video](https://youtu.be/ajgAGF-rmtE)   **Classification and Regression Trees** The *Classification and Regression Trees* procedure implements a machine-learning process to predict observations from data. It creates models of 2 forms: 1. *Classification models* that divide observations into groups based on their observed characteristics. 1. *Regression models* that predict the value of a dependent variable. The models are constructed by creating a tree, each node of which corresponds to a binary decision. Given a particular observation, one travels down the branches of the tree until a terminating leaf is found. Each leaf of the tree is associated with a predicted class or value. 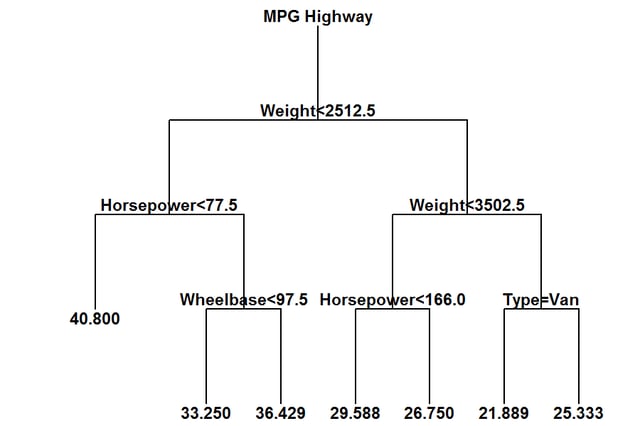![cart.png](https://www.statgraphics.com/hs-fs/hubfs/cart.png?width=640&name=cart.png "cart.png") More: [Classification and Regression Trees.pdf](https://www.statgraphics.com/hubfs/PDFs/Classification_and_Regression_Trees.pdf?t=1506731285692)   **Piecewise Linear Regression (Version 19)** The *Piecewise Linear Regression* procedure is designed to fit a regression model where the relationship between the dependent variable Y and the independent variable X is a continuous function consisting of 2 or more linear segments. The function is estimated using nonlinear least squares. The user specifies the number of segments and initial estimates of the locations where the segments join. 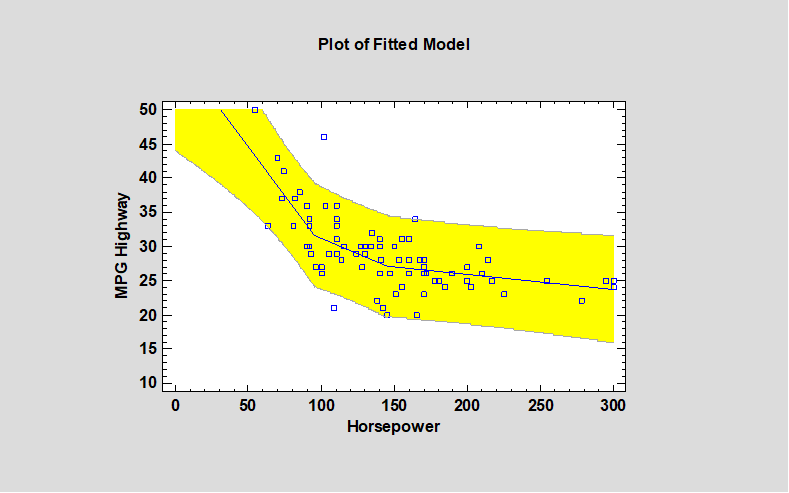![piecewise-1](https://www.statgraphics.com/hs-fs/hubfs/piecewise-1.png?width=789&name=piecewise-1.png)More: [Piecewise Linear Regression.pdf](https://www.statgraphics.com/hubfs/Piecewise%20Linear%20Regression.pdf) or [watch video](https://www.youtube.com/watch?v=QINYtCKtpEw&t=24s)   **Quantile Regression (Version 19)** The *Quantile Regression* procedure fits linear models to describe the relationship between selected quantiles of a dependent variable Y and one or more independent variables. The independent variables may be either quantitative or categorical. Unlike standard multiple regression procedures in which the model is used to predict the mean response, quantile regression models may be used to predict any percentile. Median regression is a special case where the quantile to be predicted is the 50th percentile. 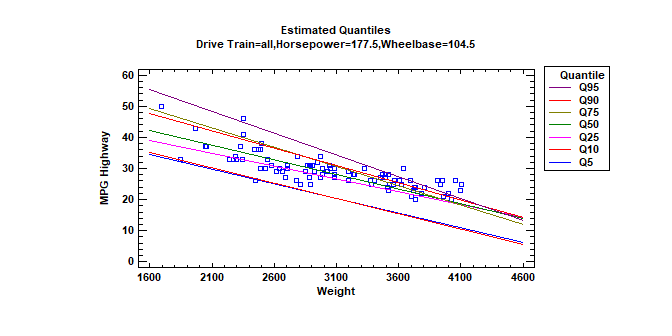![quantreg](https://www.statgraphics.com/hs-fs/hubfs/quantreg.png?width=672&name=quantreg.png)More: [Quantile Regression.pdf](https://www.statgraphics.com/hubfs/Quantile%20Regression.pdf)   **Stability Studies (Version 19)** Stability studies are commonly used by pharmaceutical companies to estimate the rate of drug degradation and to establish shelf life. Measurements are typically made on samples from multiple batches at different points in time. Of primary interest is estimating the time at which the lower prediction limit from the degradation model crosses the lower specification limits for the drug. Depending on the structure of the data, batches may be treated as either a fixed or random factor. 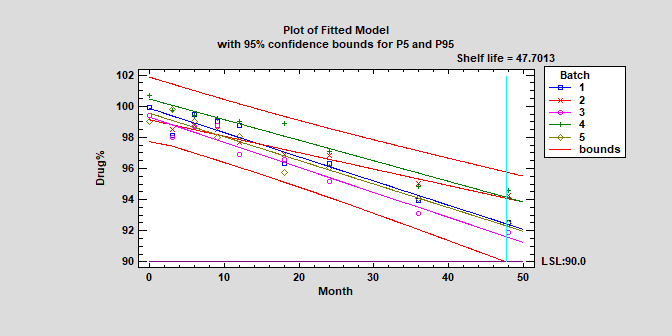![stability-1](https://www.statgraphics.com/hs-fs/hubfs/stability-1.png?width=672&name=stability-1.png) More: [Stability Study.pdf](https://www.statgraphics.com/hubfs/Stability%20Study.pdf)or [Watch Video](https://youtu.be/gm5POKYVLq8) **Zero-Inflated Count Regression (Version 19)** The *Zero Inflated Count Regression* procedure is designed to fit a regression model in which the dependent variable *Y* consists of counts. The fitted regression model relates *Y* to one or more predictor variables *X*, which may be either quantitative or categorical. It is similar to the procedures for *Poisson Regression* and *Negative Binomial Regression* except that it contains an additional component that represents the occurrence of more zeroes than would be expected in those models. Data containing excess zeroes is very common, including such diverse examples as the number of days a student is absent from school, the number of insurance claims within a population where not everyone has insurance, the number of defects in a manufactured item, and wild animal counts. ![zip-1](https://www.statgraphics.com/hs-fs/hubfs/zip-1.png?width=672&name=zip-1.png) More: [Zero-Inflated Count Regression.pdf](https://www.statgraphics.com/hubfs/Zero%20Inflated%20Count%20Regression.pdf)or [Watch Video](https://youtu.be/jUT5FOB3OOg) [![Start Using Statgraphics Today!](https://no-cache.hubspot.com/cta/default/402067/c789137b-a473-4625-b762-f58a173c4a21.png)](https://cta-redirect.hubspot.com/cta/redirect/402067/c789137b-a473-4625-b762-f58a173c4a21) [![contact-icon](https://www.statgraphics.com/hs-fs/hubfs/stat19web/sales.png?width=50&name=sales.png "contact-icon.fw")](https://www.statgraphics.com/contact-us-dealers-global-partners) ### [CONTACT SALES](https://www.statgraphics.com/contact-us-dealers-global-partners) Contact our Sales team today [![youtube-icon.fw](https://www.statgraphics.com/hubfs/stat19web/watchr.png)](https://www.statgraphics.com/instructional-videos) ### [WATCH A VIDEO](https://www.statgraphics.com/instructional-videos) Learn more about the many enhancements added to Version 19 [![download](https://www.statgraphics.com/hubfs/stat19web/downloadr.png)](https://www.statgraphics.com/download18) ### [DOWNLOAD TRIAL](https://www.statgraphics.com/download19) Try Statgraphics 19 today for free! [![eye icon](https://www.statgraphics.com/hubfs/stat19web/viewr.png)](https://www.statgraphics.com/download-brochure-0) ### [VIEW BROCHURE](https://www.statgraphics.com/download-brochure-0) Discover Statgraphics 19 with our product brochure. ![contact us](https://www.statgraphics.com/hubfs/stat19web/contactr.png) © 2025 Statgraphics Technologies, Inc. The Plains, Virginia [CONTACT US](https://www.statgraphics.com/contact-us-partner) ![Statgraphics download center](https://www.statgraphics.com/hs-fs/hubfs/stat19web/downloadcr.png?width=50&name=downloadcr.png) Have you purchased Statgraphics Centurion or Sigma Express and need to download your copy? [CLICK HERE](https://www.statgraphics.com/download-center) - [Support](https://www.statgraphics.com/customer-support-overview) - [Company](https://www.statgraphics.com/contact-us-dealers-global-partners) - [Blog](https://blog.statgraphics.com)