--- title: Standard deviation and other essential procedures | Statgraphics description: Standard deviation, quality assurance, data analysis all made simple with these basic procedures and methods. Visit Statgraphics to get more information! --- [![Statgraphics 19 logo](https://www.statgraphics.com/hs-fs/hubfs/stat19plain-01-1.png?width=2272&height=484&name=stat19plain-01-1.png "Statgraphics 19 logo")](https://www.statgraphics.com) - [Products](https://www.statgraphics.com/product) - [Learn](https://www.statgraphics.com/statistics-library) - [Training](https://www.statgraphics.com/training-and-consulting) - [Product](https://www.statgraphics.com/product) - [Centurion XVIII](https://www.statgraphics.com/centurion-xvii) - [Sigma Express](https://www.statgraphics.com/statgraphics-sigma-express) - [Online](https://www.statgraphics.com/statgraphics-stratus) - [Web Services](https://www.statgraphics.com/statgraphics-web-services) - [Learn](https://www.statgraphics.com/statistics-library) - [Statistics Library](https://www.statgraphics.com/statistics-library) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Instructional Videos](https://www.statgraphics.com/instructional-videos) - [Applications/ Case Studies](https://www.statgraphics.com/application) - [Training & Consulting](https://www.statgraphics.com/training-and-consulting) - [Statpoint Seminars](https://www.statgraphics.com/statpoint-seminar) - [Statpoint Instructors](https://www.statgraphics.com/statpoint-instructor) - [Training Partners](https://www.statgraphics.com/training-partners) - [Webinars](https://www.statgraphics.com/webinars) - [Support](https://www.statgraphics.com/customer-support-overview) - [Blog](https://www.statgraphics.com/blog) - [Store](http://store.statgraphics.com) ### Statgraphics ## [Centurion](https://www.statgraphics.com/centurion-overview) #### [LEARN MORE](https://www.statgraphics.com/centurion-overview) ### Statgraphics ## [Sigma *express*](https://www.statgraphics.com/statgraphics-sigma-express) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-sigma-express) ### Statgraphics ## [*Stratus*](https://www.statgraphics.com/statgraphics-stratus) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-stratus) ### Statgraphics ## [Web Services](https://www.statgraphics.com/statgraphics-web-services) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-web-services) ## [Statistics Library](https://www.statgraphics.com/statistics-library) #### [LEARN MORE](https://www.statgraphics.com/statistics-library) ## [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) #### [LEARN MORE](https://www.statgraphics.com/six-sigma-lean) ## [Instructional Videos](https://www.statgraphics.com/instructional-videos) #### [LEARN MORE](https://www.statgraphics.com/instructional-videos) ## [Applications/ Case Studies](https://www.statgraphics.com/statistical-applications) #### [LEARN MORE](https://www.statgraphics.com/statistical-applications) ## [Statgraphics Seminars](https://www.statgraphics.com/statpoint-seminar) #### [LEARN MORE](https://www.statgraphics.com/statpoint-seminar) ## [Statgraphics Instructors](https://www.statgraphics.com/statpoint-instructor) #### [LEARN MORE](https://www.statgraphics.com/statpoint-instructor) ## [Training Partners](https://www.statgraphics.com/public-seminar) #### [LEARN MORE](https://www.statgraphics.com/public-seminar) ## [Webinars](https://www.statgraphics.com/webinars) #### [LEARN MORE](https://www.statgraphics.com/webinars) #### Statistical Capabilities - [Analysis of Variance](https://www.statgraphics.com/analysis-of-variance) - [Basic Statistical Methods](https://www.statgraphics.com/basic-statistical-methods) - [Categorical Data Analysis](https://www.statgraphics.com/categorical-data-analysis) - [Data Mining & Machine Learning](https://www.statgraphics.com/data-mining) - [Design of Experiments](https://www.statgraphics.com/design-of-experiments) - [Exploratory Data Analysis](https://www.statgraphics.com/exploratory-data-analysis) - [Life Data Analysis & Reliability](https://www.statgraphics.com/life-data-analysis-and-reliability) - [Measurement Systems Analysis](https://www.statgraphics.com/measurement-systems-analysis) - [Monte Carlo Simulation](https://www.statgraphics.com/monte-carlo) - [Multivariate Methods](https://www.statgraphics.com/multivariate-methods) - [Nonparametric Methods](https://www.statgraphics.com/nonparametric-methods) - [Probability Distributions](https://www.statgraphics.com/probability-distributions) - [Process Capability Analysis](https://www.statgraphics.com/process-capability-analysis) - [Regression Analysis](https://www.statgraphics.com/regression-analysis) - [Sample Size Determination](https://www.statgraphics.com/sample-size-determination) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Statistical Process Control Charts](https://www.statgraphics.com/statistical-process-control-charts) - [Time Series Analysis & Forecasting](https://www.statgraphics.com/time-series-analysis-and-forecasting) - [Visualization](https://www.statgraphics.com/visualization) # Basic Statistical Methods Statpoint Technologies products provide a wide range of procedures for accomplishing basic statistical tasks.This section describes some procedures in our basic statistics software for handling data sampled from one or more populations: [![Start Using Statgraphics Today!](https://no-cache.hubspot.com/cta/default/402067/c789137b-a473-4625-b762-f58a173c4a21.png)](https://cta-redirect.hubspot.com/cta/redirect/402067/c789137b-a473-4625-b762-f58a173c4a21) | Procedure | Statgraphics Centurion 18/19 | Statgraphics Sigma *express* | Statgraphics *stratus* | Statgraphics Web Services | StatBeans | | --- | --- | --- | --- | --- | --- | | [One Sample Analysis](https://www.statgraphics.com/basic-statistical-methods#One%20Sample%20Analysis) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Outlier Identification](https://www.statgraphics.com/basic-statistical-methods#Outlier%20Identification) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Comparing Two Independent Samples](https://www.statgraphics.com/basic-statistical-methods#Comparing%20Two%20Independent%20Samples) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Comparing Two Paired Samples](https://www.statgraphics.com/basic-statistical-methods#Comparing%20Two%20Paired%20Samples) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Comparing Multiple Samples](https://www.statgraphics.com/basic-statistical-methods#Comparing%20Multiple%20Samples) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Comparing Rates and Proportions](https://www.statgraphics.com/basic-statistical-methods#Comparing%20Rates%20and%20Proportions) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Equivalence and Noninferiority Tests for Means](https://www.statgraphics.com/basic-statistical-methods#Equivalence) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Equivalence and Noninferiority Tests for Variances](https://www.statgraphics.com/basic-statistical-methods#equivvar)(V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Power Transformations](https://www.statgraphics.com/basic-statistical-methods#Power) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   | #### One Sample Analysis The One Variable Analysis procedure is one of the primary procedures for analyzing a single column of numeric data. It calculates summary statistics and confidence intervals, performs hypothesis tests, and creates a variety of graphical displays. The graphs include a scatterplot, histogram, box-and-whisker plot, quantile plot, normal probability plot, density trace, and symmetry plot. The tables include percentiles and a stem-and-leaf display.  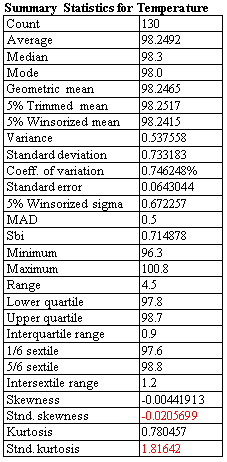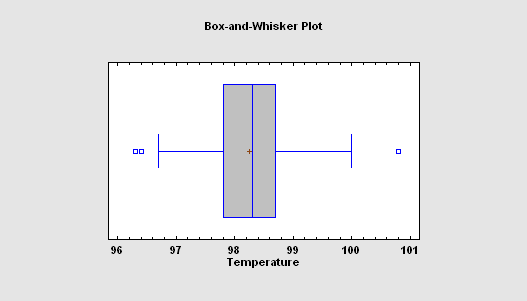![stats.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/stats.png?width=227&height=462&name=stats.png) ![onebox.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/onebox.png?width=640&name=onebox.png "onebox.png") More:[One Variable Analysis.pdf](https://www.statgraphics.com/hubfs/PDFs/One_Variable_Analysis_1-1.pdf)   #### Outlier Identification The Outlier Identification procedure is designed to help determine whether or not a sample of n numeric observations contains outliers. Outliers are observations that do not come from the same distribution as the rest of the sample. Both graphical methods and formal statistical tests due to Grubbs and Dixon are included. The procedure will also save a column of flags identifying the outliers in a form that can be used to exclude those observations when running other procedures. 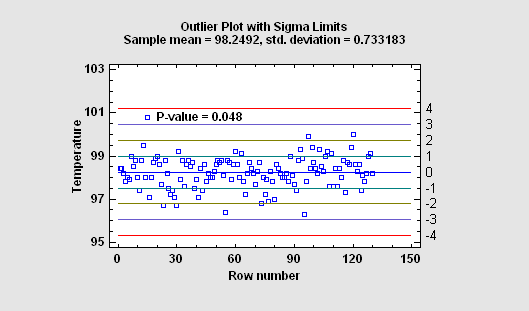![outlier.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/outlier.png?width=640&name=outlier.png "outlier.png") More: [Outlier Identification.pdf](https://www.statgraphics.com/hubfs/PDFs/Outlier_Identification-1.pdf)   #### Two Sample Comparison The Two Sample Comparison procedure is designed to compare two independent samples of variable data. Tests are run to determine whether or not there are significant differences between the means, variances, and/or medians of the populations from which the samples were taken. In addition, the data may be displayed graphically in various ways, including a dual histogram, a multiple box-and-whisker plot, and a quantile-quantile plot. 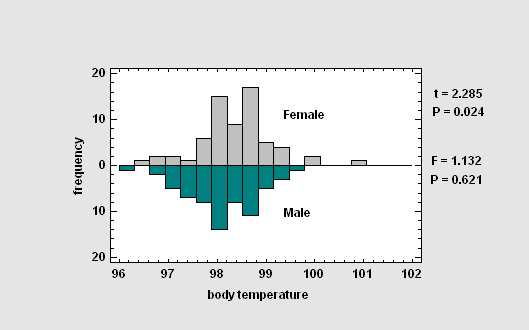![twosam.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/twosam.png?width=640&name=twosam.png "twosam.png") More:[Two Sample Comparison.pdf](https://www.statgraphics.com/hubfs/PDFs/Two_Sample_Comparison_1-1.pdf)   #### Paired Sample Comparison The Paired Sample Comparison procedure is designed to compare data in 2 numeric columns where the values in each row are paired, i.e., correspond to the same subject or experimental unit. The primary reason for such a comparison is typically to determine whether or not the factor that differentiates the columns has a significant effect on the data. ![paired.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/paired.png?width=366&height=355&name=paired.png) More:[Paired Sample Comparison.pdf](https://www.statgraphics.com/hubfs/PDFs/Paired_Sample_Comparison-1.pdf)   #### Multiple Sample Comparison The Multiple Sample Comparison procedure is designed to compare two or more independent samples of variable data. Tests are run to determine whether or not there are significant differences between the means, variances, and/or medians of the populations from which the samples were taken. In addition, the data may be displayed graphically in various ways, including a multiple scatterplot, a means plot, an ANOM plot, and a medians plot. 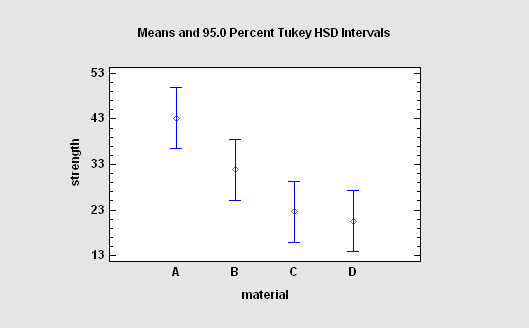![oneway.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/oneway.png?width=640&name=oneway.png "oneway.png") More: [Multiple Sample Comparison.pdf](https://www.statgraphics.com/hubfs/PDFs/Multiple_Sample_Comparison.pdf)   #### Comparison of Rates and Proportions Procedures are also available for comparing the observed rates of an event amongst k samples (based on a Poisson distribution), or comparing the observed proportions (based on a binomial distribution). Tests provided include a dispersion test, a chi-square test, and a likelihood ratio test. The procedures also perform an analysis of means (ANOM) to determine which samples differ significantly from the overall average. 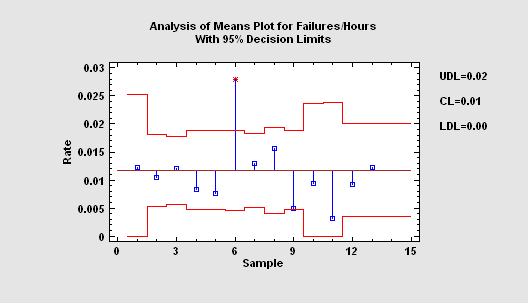![anom.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/anom.png?width=640&name=anom.png "anom.png") More: [Comparison of Rates.pdf,](https://www.statgraphics.com/hubfs/PDFs/Comparison_of_Rates.pdf)[Comparison of Proportions.pdf](https://www.statgraphics.com/hubfs/PDFs/Comparison_of_Proportions.pdf)   #### Equivalence and Noninferiority Tests for Means Four procedures are available to demonstrate equivalence (two-sided) or noninferiority (one-sided) of means. They are used to compare 2 independent means, compare 2 paired means, compare a single mean against a target value, and analyze the results of a 2x2 crossover study. Unlike standard hypothesis tests which are designed to prove superiority of one method over another, equivalence tests are designed to prove that two methods have essentially the same mean.  ![equivalence4.png](https://www.statgraphics.com/hs-fs/hubfs/equivalence4.png?width=640&name=equivalence4.png "equivalence4.png") More: [Equivalence & Noninferiority Tests (Comparing Mean to Target).pdf](https://www.statgraphics.com/hubfs/PDFs/Equivalence_%26_Noninferiority_Tests_(Comparing_Mean_to_Target).pdf), [Equivalence & Noninferiority Tests (Comparing Two Means).pdf](https://www.statgraphics.com/hubfs/PDFs/Equivalence_%26_Noninferiority_Tests_(Comparing_Two_Means).pdf), [Equivalence & Noninferiority Tests (Comparing Paired Samples).pdf](https://www.statgraphics.com/hubfs/PDFs/Equivalence_%26_Noninferiority_Tests_(Comparing_Paired_Samples).pdf), [Equivalence & Noninferiority Tests (2x2 Crossover Study).pdf](https://www.statgraphics.com/hubfs/PDFs/Equivalence_%26_Noninferiority_Tests_(2x2_Crossover_Study).pdf) or [Watch Videos Part 1: 2 Independent Samples](https://youtu.be/-PK0zwbhFcM), [Part 2: 2x2 Crossover Studies](https://youtu.be/s8gNCA9IRdo) #### Equivalence and Noninferiority Tests for Variances (Version 19) Two procedures are available to demonstrate equivalence (two-sided) or noninferiority (one-sided) of variances. They are used to compare 2 independent variances and to compare a single variance to a target value. Unlike standard hypothesis tests which are designed to prove superiority of one method over another, equivalence tests are designed to prove that two methods have essentially the same variance.   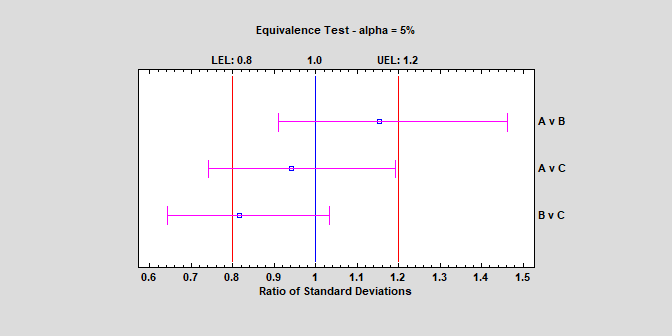[Watch Video](https://www.youtube.com/watch?v=Pdv-rsvEJ28) ![equivar](https://www.statgraphics.com/hs-fs/hubfs/equivar.png?width=672&name=equivar.png) More: [Equivalence & Noninferiority Tests (Comparing Variance to Target).pdf](https://www.statgraphics.com/hubfs/Equivalence%20%26%20Noninferiority%20Tests%20(Comparing%20Variance%20to%20Target).pdf), [Equivalence & Noninferiority Tests (Comparing Two Variances).pdf](https://www.statgraphics.com/hubfs/Equivalence%20%26%20Noninferiority%20Tests%20(Comparing%20Two%20Variances).pdf)   #### Power Transformations The Power Transformations procedure is designed to determine a normalizing transformation for a column of numeric observations that do not come from a normal distribution. In such cases, it is often possible to find a power transformation that will make the data approximately normal. Given such a transformation, statistical procedures that assume normality can then be applied to the transformed data. 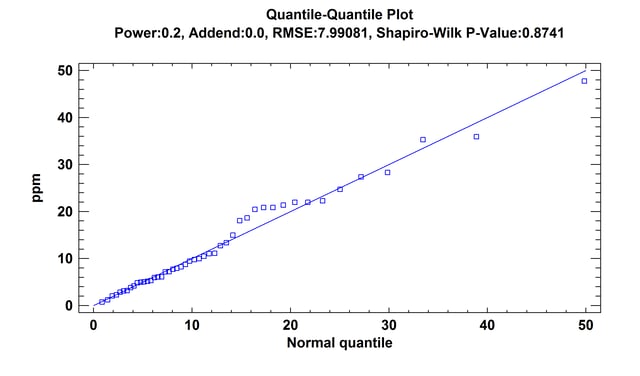![power.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/power.png?width=640&name=power.png "power.png") More: [Power Transformations.pdf](https://www.statgraphics.com/hubfs/PDFs/Power_Transformations.pdf), [Power Transformations Statlet.pdf](https://www.statgraphics.com/hubfs/PDFs/Power_Transformations_Statlet.pdf) [![Start Using Statgraphics Today!](https://no-cache.hubspot.com/cta/default/402067/c789137b-a473-4625-b762-f58a173c4a21.png)](https://cta-redirect.hubspot.com/cta/redirect/402067/c789137b-a473-4625-b762-f58a173c4a21) [![contact-icon](https://www.statgraphics.com/hs-fs/hubfs/stat19web/sales.png?width=50&name=sales.png "contact-icon.fw")](https://www.statgraphics.com/contact-us-dealers-global-partners) ### [CONTACT SALES](https://www.statgraphics.com/contact-us-dealers-global-partners) Contact our Sales team today [![youtube-icon.fw](https://www.statgraphics.com/hubfs/stat19web/watchr.png)](https://www.statgraphics.com/instructional-videos) ### [WATCH A VIDEO](https://www.statgraphics.com/instructional-videos) Learn more about the many enhancements added to Version 19 [![download](https://www.statgraphics.com/hubfs/stat19web/downloadr.png)](https://www.statgraphics.com/download18) ### [DOWNLOAD TRIAL](https://www.statgraphics.com/download19) Try Statgraphics 19 today for free! [![eye icon](https://www.statgraphics.com/hubfs/stat19web/viewr.png)](https://www.statgraphics.com/download-brochure-0) ### [VIEW BROCHURE](https://www.statgraphics.com/download-brochure-0) Discover Statgraphics 19 with our product brochure. ![contact us](https://www.statgraphics.com/hubfs/stat19web/contactr.png) © 2025 Statgraphics Technologies, Inc. The Plains, Virginia [CONTACT US](https://www.statgraphics.com/contact-us-partner) ![Statgraphics download center](https://www.statgraphics.com/hs-fs/hubfs/stat19web/downloadcr.png?width=50&name=downloadcr.png) Have you purchased Statgraphics Centurion or Sigma Express and need to download your copy? [CLICK HERE](https://www.statgraphics.com/download-center) - [Support](https://www.statgraphics.com/customer-support-overview) - [Company](https://www.statgraphics.com/contact-us-dealers-global-partners) - [Blog](https://blog.statgraphics.com) -   -           -