--- title: Statistical Probability Distributions | Examples in Statgraphics description: Statgraphics contains several procedures for manipulating probability distributions. Learn about the 45 distributions Statgraphics can plot on this web page. --- [![Statgraphics 19 logo](https://www.statgraphics.com/hs-fs/hubfs/stat19plain-01-1.png?width=2272&height=484&name=stat19plain-01-1.png "Statgraphics 19 logo")](https://www.statgraphics.com) - [Products](https://www.statgraphics.com/product) - [Learn](https://www.statgraphics.com/statistics-library) - [Training](https://www.statgraphics.com/training-and-consulting) - [Product](https://www.statgraphics.com/product) - [Centurion XVIII](https://www.statgraphics.com/centurion-xvii) - [Sigma Express](https://www.statgraphics.com/statgraphics-sigma-express) - [Online](https://www.statgraphics.com/statgraphics-stratus) - [Web Services](https://www.statgraphics.com/statgraphics-web-services) - [Learn](https://www.statgraphics.com/statistics-library) - [Statistics Library](https://www.statgraphics.com/statistics-library) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Instructional Videos](https://www.statgraphics.com/instructional-videos) - [Applications/ Case Studies](https://www.statgraphics.com/application) - [Training & Consulting](https://www.statgraphics.com/training-and-consulting) - [Statpoint Seminars](https://www.statgraphics.com/statpoint-seminar) - [Statpoint Instructors](https://www.statgraphics.com/statpoint-instructor) - [Training Partners](https://www.statgraphics.com/training-partners) - [Webinars](https://www.statgraphics.com/webinars) - [Support](https://www.statgraphics.com/customer-support-overview) - [Blog](https://www.statgraphics.com/blog) - [Store](http://store.statgraphics.com) ### Statgraphics ## [Centurion](https://www.statgraphics.com/centurion-overview) #### [LEARN MORE](https://www.statgraphics.com/centurion-overview) ### Statgraphics ## [Sigma *express*](https://www.statgraphics.com/statgraphics-sigma-express) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-sigma-express) ### Statgraphics ## [*Stratus*](https://www.statgraphics.com/statgraphics-stratus) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-stratus) ### Statgraphics ## [Web Services](https://www.statgraphics.com/statgraphics-web-services) #### [LEARN MORE](https://www.statgraphics.com/statgraphics-web-services) ## [Statistics Library](https://www.statgraphics.com/statistics-library) #### [LEARN MORE](https://www.statgraphics.com/statistics-library) ## [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) #### [LEARN MORE](https://www.statgraphics.com/six-sigma-lean) ## [Instructional Videos](https://www.statgraphics.com/instructional-videos) #### [LEARN MORE](https://www.statgraphics.com/instructional-videos) ## [Applications/ Case Studies](https://www.statgraphics.com/statistical-applications) #### [LEARN MORE](https://www.statgraphics.com/statistical-applications) ## [Statgraphics Seminars](https://www.statgraphics.com/statpoint-seminar) #### [LEARN MORE](https://www.statgraphics.com/statpoint-seminar) ## [Statgraphics Instructors](https://www.statgraphics.com/statpoint-instructor) #### [LEARN MORE](https://www.statgraphics.com/statpoint-instructor) ## [Training Partners](https://www.statgraphics.com/public-seminar) #### [LEARN MORE](https://www.statgraphics.com/public-seminar) ## [Webinars](https://www.statgraphics.com/webinars) #### [LEARN MORE](https://www.statgraphics.com/webinars) #### Statistical Capabilities - [Analysis of Variance](https://www.statgraphics.com/analysis-of-variance) - [Basic Statistical Methods](https://www.statgraphics.com/basic-statistical-methods) - [Categorical Data Analysis](https://www.statgraphics.com/categorical-data-analysis) - [Data Mining & Machine Learning](https://www.statgraphics.com/data-mining) - [Design of Experiments](https://www.statgraphics.com/design-of-experiments) - [Exploratory Data Analysis](https://www.statgraphics.com/exploratory-data-analysis) - [Life Data Analysis & Reliability](https://www.statgraphics.com/life-data-analysis-and-reliability) - [Measurement Systems Analysis](https://www.statgraphics.com/measurement-systems-analysis) - [Monte Carlo Simulation](https://www.statgraphics.com/monte-carlo) - [Multivariate Methods](https://www.statgraphics.com/multivariate-methods) - [Nonparametric Methods](https://www.statgraphics.com/nonparametric-methods) - [Probability Distributions](https://www.statgraphics.com/probability-distributions) - [Process Capability Analysis](https://www.statgraphics.com/process-capability-analysis) - [Regression Analysis](https://www.statgraphics.com/regression-analysis) - [Sample Size Determination](https://www.statgraphics.com/sample-size-determination) - [Six Sigma & Lean](https://www.statgraphics.com/six-sigma-lean) - [Statistical Process Control Charts](https://www.statgraphics.com/statistical-process-control-charts) - [Time Series Analysis & Forecasting](https://www.statgraphics.com/time-series-analysis-and-forecasting) - [Visualization](https://www.statgraphics.com/visualization) # Probability Distributions Statgraphics contains several procedures for manipulating statistical probability distributions. Each of more than 50 distributions may be plotted, fit to data, and used to calculate critical values or tail areas. Random samples may also be generated from each of the distributions with this stat software. The following procedures are provided: | Procedure | Statgraphics Centurion 18/19 | Statgraphics Sigma *express* | Statgraphics *stratus* | Statgraphics Web Services | StatBeans | | --- | --- | --- | --- | --- | --- | | [Probability Distributions](https://www.statgraphics.com/probability-distributions#Probability%20Distributions) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Sampling Distributions](https://www.statgraphics.com/probability-distributions#Sampling%20Distributions) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Normal Probability Plot](https://www.statgraphics.com/probability-distributions#Normal%20Probability%20Plot) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Probability Plots for Nonnormal Data](https://www.statgraphics.com/probability-distributions#Probability%20Plots%20for%20Nonnormal%20Data) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Distribution Fitting (Uncensored Data)](https://www.statgraphics.com/probability-distributions#Distribution%20Fitting%20(Uncensored%20Data)) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Distribution Fitting (Censored Data)](https://www.statgraphics.com/probability-distributions#Distribution%20Fitting%20(Censored%20Data)) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Distribution Fitting (Arbitrarily Censored Data)](https://www.statgraphics.com/probability-distributions#Arbitrary) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Random Number Generation](https://www.statgraphics.com/probability-distributions#Random%20Number%20Generation) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Multivariate Normal Random Numbers](https://www.statgraphics.com/probability-distributions#MVNormal) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Statistical Tolerance Limits](https://www.statgraphics.com/probability-distributions#Statistical%20Tolerance%20Limits) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) | | [Multivariate Tolerance Limits](https://www.statgraphics.com/probability-distributions#MVTol) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Univariate Mixture Distributions](https://www.statgraphics.com/probability-distributions#mix1)(V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   | | [Bivariate Mixture Distributions](https://www.statgraphics.com/probability-distributions#mix2) (V19 only) | ![](https://www.statgraphics.com/hubfs/migrated-pages-image/checkmark.png) |   |   |   |   |   #### Probability Distributions The Statgraphics Probability Distributions procedure calculates probabilities for 46 discrete and continuous distributions. The stat software will plot the probability density or mass function, cumulative distribution function, survivor function, log survivor function, or hazard function. It also calculates critical values and tail areas. Random samples may be generated from any of the distributions given specified parameters value. 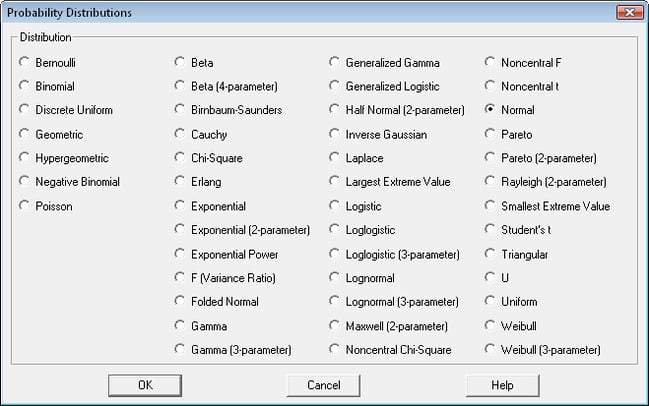![dists.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/dists.png?width=649&height=407&name=dists.png) More:[Probability Distributions.pdf](https://www.statgraphics.com/hubfs/PDFs/Probability_Distributions.pdf'%20download=)   #### Sampling Distributions The stat software's Sampling Distributions procedure calculates tail areas and critical values for the normal, Student's t, chi-square, and F distributions. It also plots the calculated results. 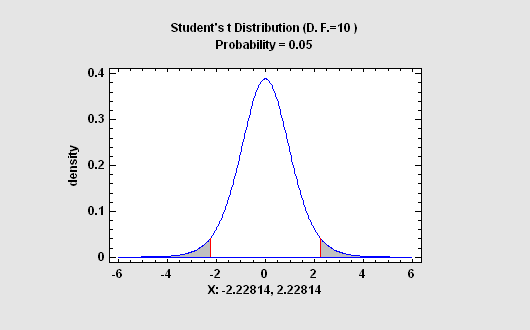![sampdist.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/sampdist.png?width=640&name=sampdist.png "sampdist.png") More:[Sampling Distributions.pdf](https://www.statgraphics.com/hubfs/PDFs/Sampling_Distributions.pdf)   #### Normal Probability Plot The Normal Probability Plot is used to help judge whether or not a sample of numeric data comes from a normal probability distribution. If it does, the points should fall close to a straight line when plotted against the specially scaled Y-axis. For non-normal data, you can often determine the type of departure from normality by examining the way in which the data deviate from the normal reference line. 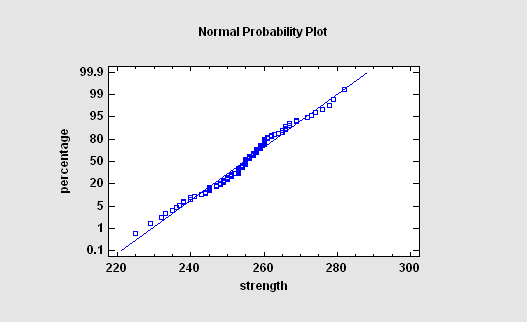![nplot_1.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/nplot_1.png?width=640&name=nplot_1.png "nplot_1.png") More:[Normal Probability Plot.pdf](https://www.statgraphics.com/hubfs/PDFs/Normal_Probability_Plot.pdf)   #### Probability Plots for Nonnormal Data The Probability Plots procedure plots the data in a single numeric column on graphs that are specifically scaled so that, if the data come from a particular distribution, the observations will fall approximately along a straight line. The procedure includes plots for the uniform, normal, lognormal, Weibull, smallest extreme value, logistic, and exponential distributions. 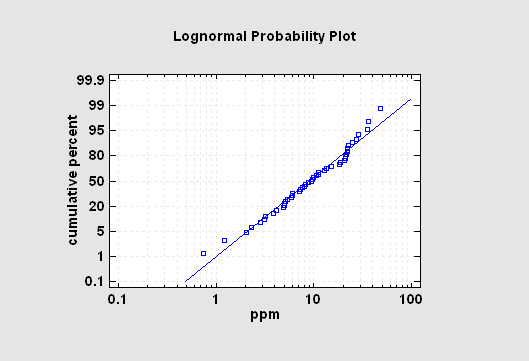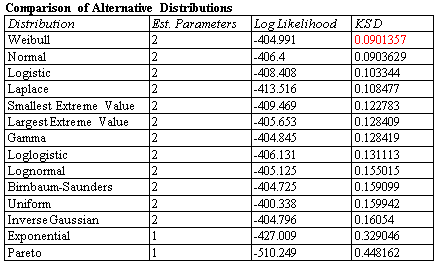![lnplot.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/lnplot.png?width=640&name=lnplot.png "lnplot.png") More: [Probability Plots.pdf](https://www.statgraphics.com/hubfs/PDFs/Probability_Plots.pdf)   #### Distribution Fitting (Uncensored Data) The Distribution Fitting (Uncensored Data) procedure fits any of 46 probability distributions to a column of numeric data. The data are assumed to be uncensored, i.e., the data represent random samples from the selected distribution. If requested, many distributions may be fit and ordered by the stat software for their ability to match the data. Goodness-of-fit tests are performed to determine which distributions adequately model the observed values. 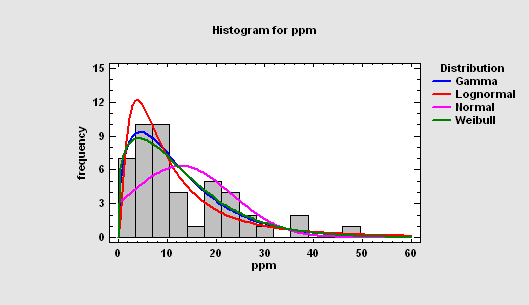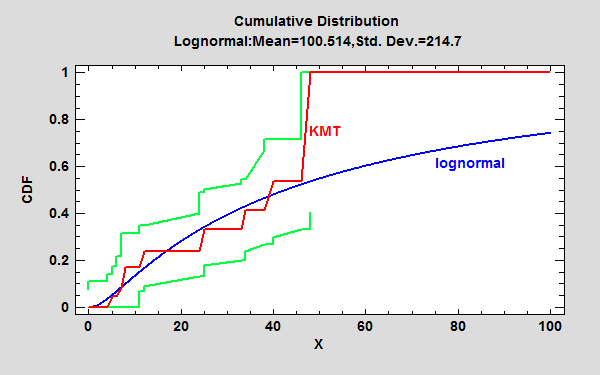![dstfit.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/dstfit.png?width=640&name=dstfit.png "dstfit.png") More:[Distribution Fitting (Uncensored Data)](https://www.statgraphics.com/hubfs/PDFs/Distribution_Fitting_Uncensored_Data_1.pdf)   #### Distribution Fitting (Censored Data) The Distribution Fitting (Censored Data) procedure fits any of 45 probability distributions to a column of censored numeric data. Censoring occurs when some of the data values are not known exactly. For example, when measuring failure times, some items under study may not have failed when the study is stopped, resulting in only a lower bound on the failure times for those items. As with uncensored data, the distributions may be sorted according to their goodness-of-fit. ![cdistfit.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/cdistfit.png?width=439&height=265&name=cdistfit.png) More: [Distribution Fitting (Censored Data)](https://www.statgraphics.com/hubfs/PDFs/Distribution_Fitting_Censored_Data_1.pdf)   #### Distribution Fitting (Arbitrarily Censored Data) The *Distribution Fitting (Arbitrarily Censored Data)* procedure analyzes data in which one or more observations are not known exactly. In particular, observations may be:  1. **Left-censored**: known only to be less than a stated value. 2. **Right-censored**: known only to be greater than a stated value. 3. **Interval censored:** known only to fall within a stated interval. The procedure calculates summary statistics, fits distributions, creates graphs, and calculates a nonparametric estimate of the survival function. ![censored.png](https://www.statgraphics.com/hs-fs/hubfs/censored.png?width=640&name=censored.png "censored.png") More: [Distribution Fitting (Arbitrarily Censored Data)](https://www.statgraphics.com/hubfs/PDFs/Distribution_Fitting_Arbitrarily_Censored_Data.pdf) or [Watch Video](https://youtu.be/k2vkuqCbmnE)   #### Random Number Generation Random numbers may be generated by the stat software from any of the 46 probability distributions using the Probability Distributions procedure. They may also be generated as part of the Monte Carlo simulations in Statgraphics Centurion. 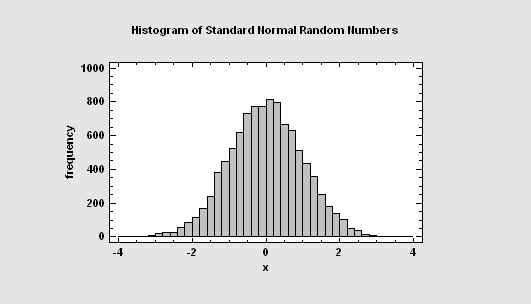![random.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/random.png?width=640&name=random.png "random.png") More:[Probability Distributions, Monte Carlo Simulation (General Simulation Models)](https://www.statgraphics.com/hubfs/PDFs/Probability_Distributions_1.pdf)   #### Multivariate Normal Random Numbers This procedure generates random numbers from a multivariate normal distribution involving up to 12 variables. The user inputs the variable means, standard deviations, and the correlation matrix. Random samples are generated which may be saved to the Statgraphics databook. 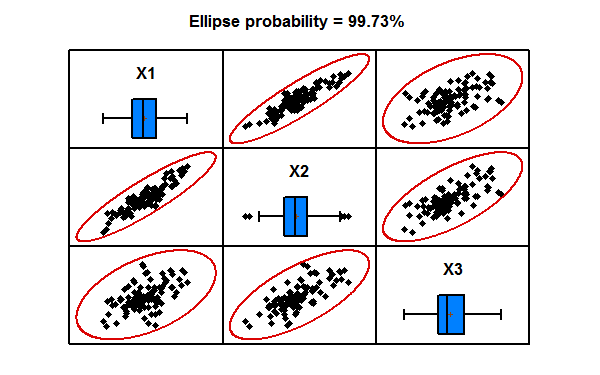![mvrandom-2.png](https://www.statgraphics.com/hs-fs/hubfs/mvrandom-2.png?width=640&name=mvrandom-2.png "mvrandom-2.png") More:[ Multivariate Normal Random Numbers](https://www.statgraphics.com/hubfs/PDFs/Multivariate_Normal_Random_Numbers.pdf)   #### Statistical Tolerance Limits Statistical tolerance limits bound a specified proportion of a population at a specified confidence level. They have many uses, including demonstrating that a large proportion of the members of a population lie within required limits. Statgraphics Centurion calculates statistical tolerance limits for 11 specific probability distributions, as well as nonparametric limits. 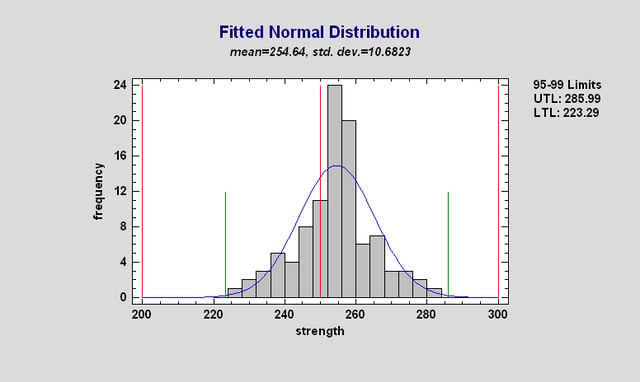![tollims.png](https://www.statgraphics.com/hs-fs/hubfs/migrated-pages-image/tollims.png?width=640&name=tollims.png "tollims.png") More:[Statistical Tolerance Limits (Observations)](https://www.statgraphics.com/hubfs/PDFs/Statistical_Tolerance_Limits_Observations.pdf)   #### Multivariate Tolerance Limits The *Multivariate Tolerance Limits* procedure creates statistical tolerance limits for data consisting of more than one variable. It includes a tolerance region that bounds a selected p% of the population with 100(1-alpha)% confidence. It also includes joint simultaneous tolerance limits for each of the variables using a Bonferroni approach. The data are assumed to be a random sample from a multivariate normal distribution. Multivariate tolerance limits are often compared to specifications for multiple variables to determine whether or not most of the population is within spec. 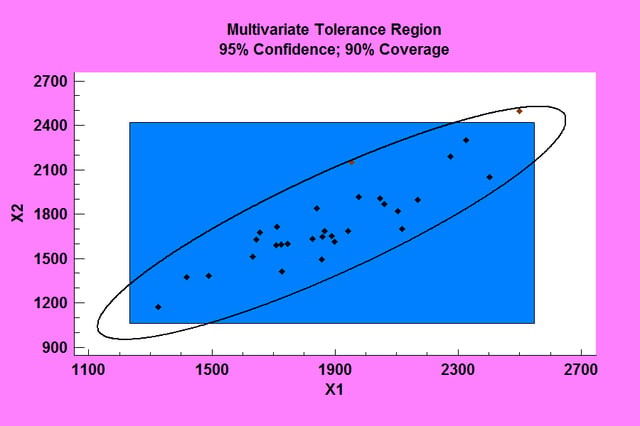![mvtolerance2.png](https://www.statgraphics.com/hs-fs/hubfs/mvtolerance2.png?width=640&name=mvtolerance2.png "mvtolerance2.png") More: [Multivariate Tolerance Limits.pdf](https://www.statgraphics.com/hubfs/PDFs/Multivariate_Tolerance_Limits.pdf?t=1505915388565) or [Watch Video](https://youtu.be/5AhO1S1IBTI)   #### Univariate Mixture Distributions (Version 19) The *Distribution Fitting (Univariate Mixture Models)* fits a distribution to continuous numeric data that consists of a mixture of 2 or more univariate Gaussian distributions. The components of the mixture may represent different groups in the sample used to fit the overall distribution, or the mixture model may approximate some distribution with a complicated shape. The procedure fits the distribution, creates graphs, and calculates tail areas and critical values. Tools are also provided for determining how many components are needed to represent a data sample. 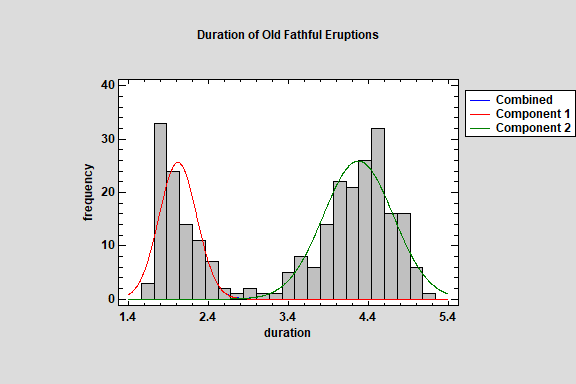![univariatemix-2](https://www.statgraphics.com/hs-fs/hubfs/univariatemix-2.png?width=576&name=univariatemix-2.png) More: [Distribution Fitting (Univariate Mixture Distributions).pdf](https://www.statgraphics.com/hubfs/Distribution%20Fitting%20(Univariate%20Mixture%20Distributions).pdf) or [Watch Video](https://www.youtube.com/watch?v=oc05CW3vBmo&t=41s)   #### Bivariate Mixture Distributions (Version 19) The *Distribution Fitting (Bivariate Mixture Distributions)* procedure fits a distribution to continuous numeric data that consists of a mixture of 2 or more bivariate Gaussian distributions. The components of the mixture may represent different groups in the sample used to fit the overall distribution, or the mixture model may approximate some distribution with a complicated shape. The procedure fits the distribution and creates graphs of the fitted model. Tools are also provided for determining how many components are needed to represent a data sample. 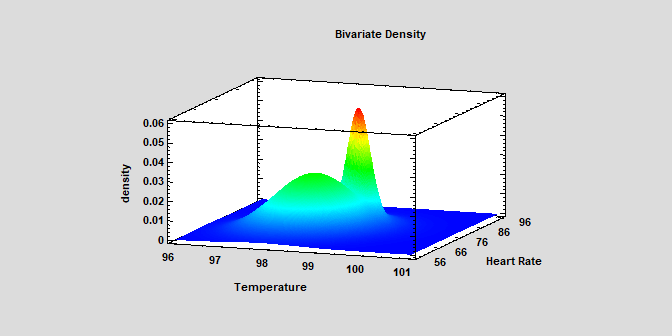![bivariatemix](https://www.statgraphics.com/hs-fs/hubfs/bivariatemix.png?width=672&name=bivariatemix.png) More: [Distribution Fitting (Bivariate Mixture Distributions).pdf](https://www.statgraphics.com/hubfs/Distribution%20Fitting%20(Bivariate%20Mixture%20Distributions).pdf) or [Watch Video](https://www.youtube.com/watch?v=UoU-j2Me0zU&t=12s) [![contact-icon](https://www.statgraphics.com/hs-fs/hubfs/stat19web/sales.png?width=50&name=sales.png "contact-icon.fw")](https://www.statgraphics.com/contact-us-dealers-global-partners) ### [CONTACT SALES](https://www.statgraphics.com/contact-us-dealers-global-partners) Contact our Sales team today [![youtube-icon.fw](https://www.statgraphics.com/hubfs/stat19web/watchr.png)](https://www.statgraphics.com/instructional-videos) ### [WATCH A VIDEO](https://www.statgraphics.com/instructional-videos) Learn more about the many enhancements added to Version 19 [![download](https://www.statgraphics.com/hubfs/stat19web/downloadr.png)](https://www.statgraphics.com/download18) ### [DOWNLOAD TRIAL](https://www.statgraphics.com/download19) Try Statgraphics 19 today for free! [![eye icon](https://www.statgraphics.com/hubfs/stat19web/viewr.png)](https://www.statgraphics.com/download-brochure-0) ### [VIEW BROCHURE](https://www.statgraphics.com/download-brochure-0) Discover Statgraphics 19 with our product brochure. ![contact us](https://www.statgraphics.com/hubfs/stat19web/contactr.png) © 2025 Statgraphics Technologies, Inc. The Plains, Virginia [CONTACT US](https://www.statgraphics.com/contact-us-partner) ![Statgraphics download center](https://www.statgraphics.com/hs-fs/hubfs/stat19web/downloadcr.png?width=50&name=downloadcr.png) Have you purchased Statgraphics Centurion or Sigma Express and need to download your copy? [CLICK HERE](https://www.statgraphics.com/download-center) - [Support](https://www.statgraphics.com/customer-support-overview) - [Company](https://www.statgraphics.com/contact-us-dealers-global-partners) - [Blog](https://blog.statgraphics.com) -   -           -